2024华为软件精英挑战赛

首先祝贺蒟蒻小队"星月湖"（话说为啥ikaros每次起名字都是这种风格啊喂!!!），经过了3.7-3.22共计2 weeks 1 day的折磨，凭着亿点点运气获得武长赛区30名的成绩，进入复赛。🥹🎉🥳

下面将记录一下suki whu sakura同学（也就是insomnia本睡不醒啦~！），在这次比赛中遇到了什么奇奇怪怪又还算有意思的经历吧~（其实是不吐不快了，逃~

任务书

对任务书的思考

看完任务书，我们主要思考的方向是

机器人寻路算法
机器人避障算法（为了让机器人之间互相不碰撞）
机器人拾取货物的策略
船选择泊位的策略
船何时开船前往虚拟点的策略
船在泊位之间轮转的策略
针对特定地图优化的策略

关于跳帧、碰撞问题

题目中要求每帧必须在15ms内处理完成并发送OK，否则在没有收到OK前，判题器将不会继续输入场面帧信息，若处理超过了15ms，那么以判题器接受到OK的时刻为准，判题器输入的帧信息的序号就可能发生不连续的情况。

如果发生跳帧，那么就会丢失掉某一帧的场面信息，如果该帧恰好判题器向场地中随机添加了一些货物，那么这部分货物信息就被永远丢失掉了，这对分数影响是巨大的。我们应该保证，即使在15ms内没能处理完所有机器人的计算操作（主要是寻路），也应该在帧耗时接近15ms的时候输出OK，并接受下一帧的场面信息，让没能处理完的计算操作在后台继续执行，只需要在使用时检查计算结果是否可用就好了。

而对于碰撞，发生碰撞后会使得机器人进入长度为20帧的RECOVERING状态，这段时间内机器人无法响应任何操作，很显然发生碰撞也是纯亏的操作，所以我们应该保证不会发生碰撞。

关于寻路算法

寻路算法有单源最短路径和多源最短路径之分，我们一开始的思路就是单源最短路径中的A*算法，这个算法在最差情况下会退化到dijkstra算法，也就是最差时间复杂度为 $O(n\log n)$ ，因为觉得多源最短路径是要 $O(n^3)$ 时间复杂度，所以可能来不及在初始化的时候搞定，后面使用了泛洪算法求地图上的连通块与到某一点的距离，发现其实dfs遍历一整遍地图也耗时不大，初始化的5s其实大有可为（但截至目前也没有想到什么很好的办法）。

我们的A*算法的代码如下：

cpp
// 启发式函数：曼哈顿距离
int PathFinder::HeuristicCostEstimate(int current_x, int current_y, int goal_x, int goal_y) {
    return abs(current_x - goal_x) + abs(current_y - goal_y);
}

// 判断移动是否合法
bool PathFinder::IsValidMove(int x, int y) { return world.originMap.isAccess(x, y); }

// A*搜索算法
Path PathFinder::FindPath(int sx, int sy, int ex, int ey) {
    //起止点相同，不进入寻路
    if(sx == ex && sy == ey){
        return {};
    }

    //不存在缓存地图，进入寻路
    std::priority_queue<Node, std::vector<Node>, std::greater<Node>> open_set;
    std::vector<std::vector<bool>> closed_set(utils::MAP_SIZE, std::vector<bool>(utils::MAP_SIZE, false));

    open_set.push(Node(sx, sy, 0, HeuristicCostEstimate(sx, sy, ex, ey), {}));

    while (!open_set.empty()) {
        Node current = open_set.top();
        open_set.pop();

        if (current.x == ex && current.y == ey) {
            return current.path;
        }

        if (closed_set[current.x][current.y]) {
            continue;
        }

        closed_set[current.x][current.y] = true;

        for (const auto &dir: directions) {
            int new_x = current.x + dir[0];
            int new_y = current.y + dir[1];

            if (IsValidMove(new_x, new_y)) {
                int new_cost = current.cost + 1;
                int heuristic = HeuristicCostEstimate(new_x, new_y, ex, ey);

                Path new_path = current.path;
                new_path.push_back((dir[0] == 0 && dir[1] == 1)    ? utils::Direction::RIGHT
                                   : (dir[0] == 0 && dir[1] == -1) ? utils::Direction::LEFT
                                   : (dir[0] == -1 && dir[1] == 0) ? utils::Direction::UP
                                                                   : utils::Direction::DOWN);

                open_set.push(Node(new_x, new_y, new_cost, heuristic, new_path));
            }
        }
    }

    return {}; // 未找到路径
}

可以看到，这里面还是存在着许多可以优化的地方的，比如std::vector<bool>的使用，熟悉STL的同学应该知道，std::vector<bool>其实并不是bool的vector，STL中对std::vector<bool>做了特化，对bool类型做了个proxy，使用了一个代理类，所以实际上凡是使用std::vector<bool>的地方，都应该想想是否可以使用bool []作为替代。

其次，这里面存在着大量的拷贝操作，每次操作current.path的时候，将会产生一次拷贝，而path是一个vector<utils::Direction>，所以将会产生不必要的性能消耗。事实上，可以记录一个每个节点的parents节点，这样可以通过对终点的回溯找到路径，解决发生大量拷贝的问题。

再次，这里对Path类型使用了vector<utils::Direction>的实现，这里让我们在后面的开发产生了产生了巨大的不便与潜在问题。后来想想，这里就应该使用vector<Position>的，每一个节点应该是一个包含x、y的位置，而后在输出的时候将两个位置的坐标做比对得到移动方向。如果在寻路的时候直接得到的就是一个vector<utils::Direction>的话，那么后续就永远丢失掉了机器人的坐标位置了，一旦发生跳帧、移动执行失败等错误，那么整个Path就不正确了，那就只能重新寻路了，这样会让整个程序显得不那么优雅。或许这就是“永远不要提早优化”的含义吧。

最后就是可读性问题，这次我们的coding习惯感觉还是存在很大的差异的，包括命名方式、对git的使用，对.clangformat的使用等等。考虑在之后写单独的文章介绍一些在ubuntu下的一些开发标准。

关于如何保证不发生碰撞——机器人避障算法

机器人避障是一个复杂的话题，不过总体来说，有两种思路，一种是考虑每个机器人在移动的时候进行试探观察，另一种是考虑对所有机器人的路径做整体调整规划。

碰撞的两种可能性

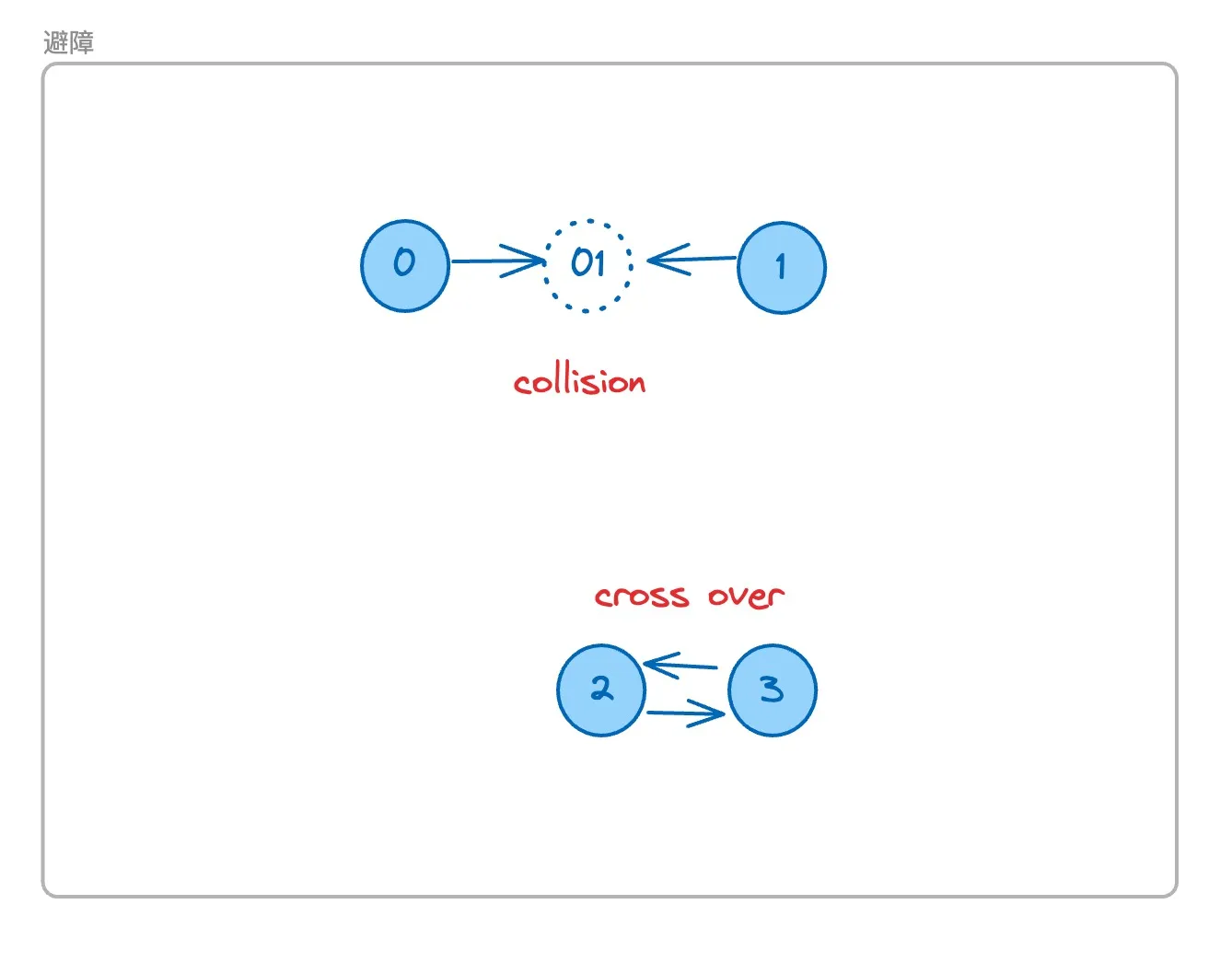
CleanShot 2024-03-26 at 15.34.17.jpg

对于机器人来说，碰撞只会存在两种可能性，第一种是两个机器人在下一帧时将会移动到同一个位置，我们可以称为collision；第二种是两个机器人在下一帧将会交换位置互相穿过，我们称为cross over

而对于机器人2下一帧将会移动到机器人3这一帧的位置，机器人3下一帧将会移动到其他方向的位置，这种情况认为是合法的，因为实际在移动操作中是不考虑输出指令的先后顺序的，判题器会视为所有机器人同时移动。

通过试探观察进行避障

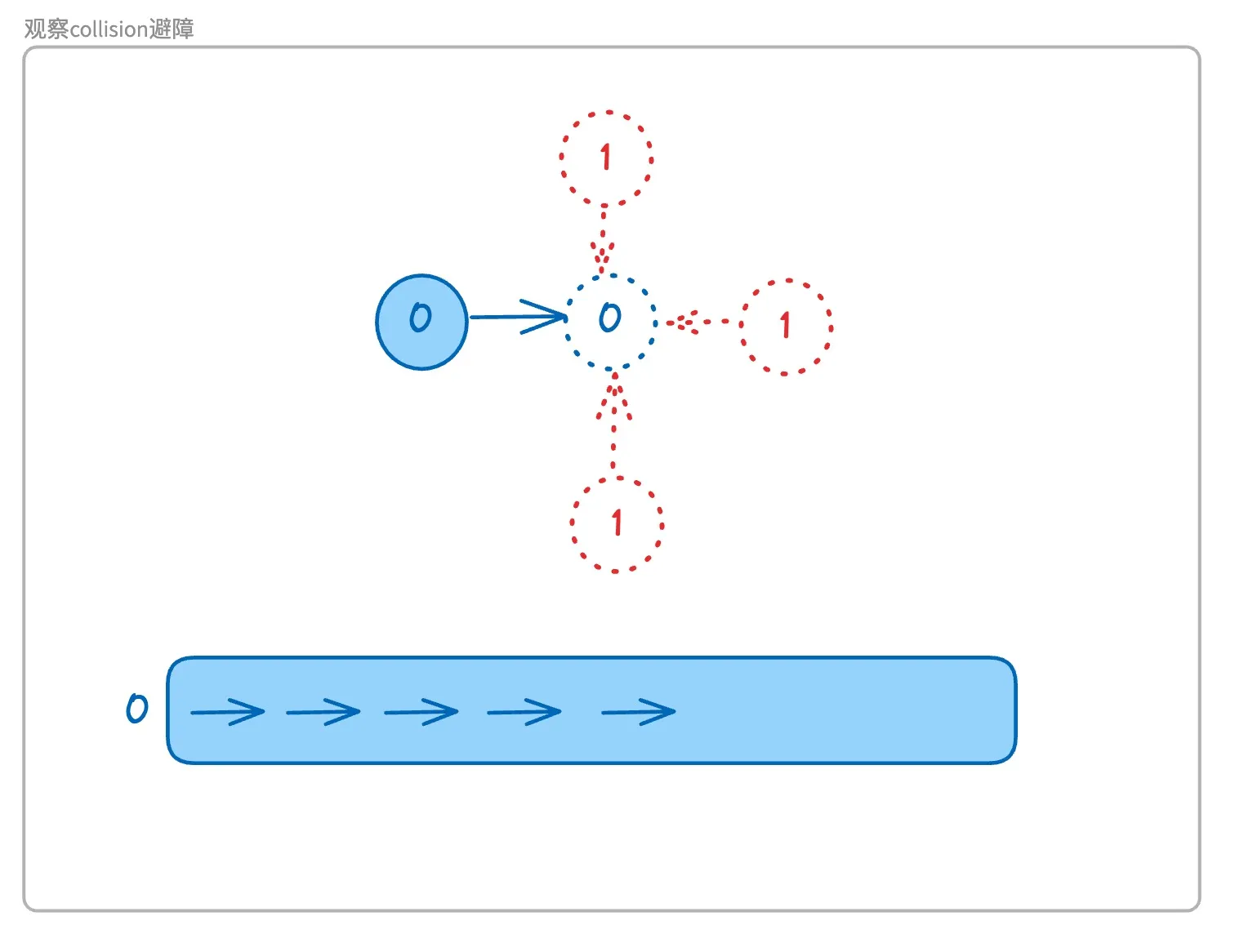
CleanShot 2024-03-26 at 19.13.43.jpg

如果机器人0的路径列表是五个向右走的话（列表里存的节点实现到底是方向还是坐标这点并不要紧），那么在进行第一步行走的时候，0号机器人应该要查看右侧蓝色虚线标注的0号位置的上下右三个方向是否有机器人，如果有机器人的话，该机器人假设是1号机器人，如果正好也要移动到蓝色虚线标注的0号位置的话，那么就判断会发生collision。解决办法则是让0号机器人呆在原地静止一帧。

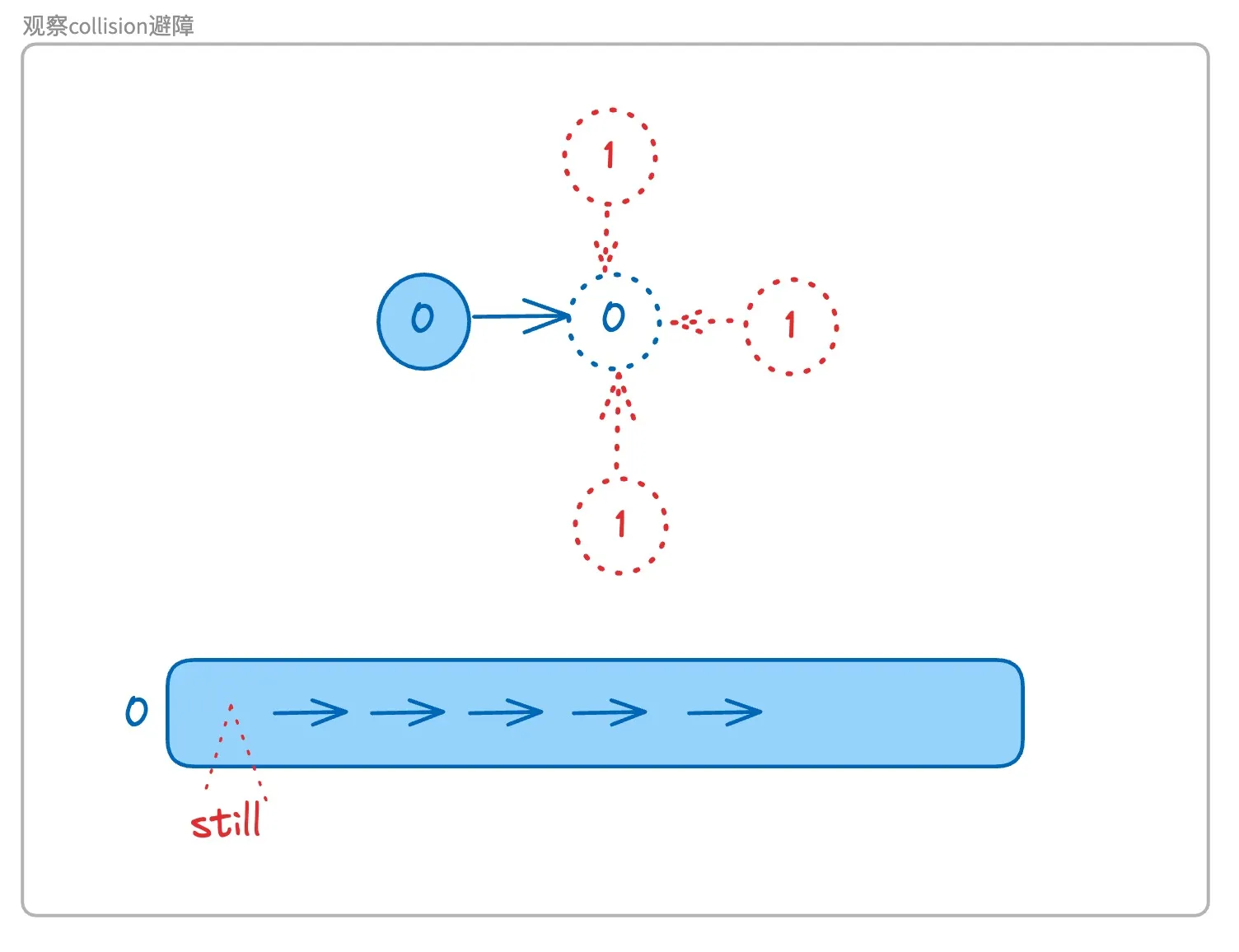
CleanShot 2024-03-26 at 19.22.50.jpg

这里要思考的点是，选择呆在原地静止一帧能不能解决问题，与选择呆在原地静止一帧会导致什么。

0号机器人在原地静止一帧后，1号机器人就会占据蓝色虚线标注的0号位置，那么在下一帧，1号机器人如果向左走，则会触发0号机器人和1号机器人的cross over，如果往上或者往下走，那么0号机器人就可以正常移动了。

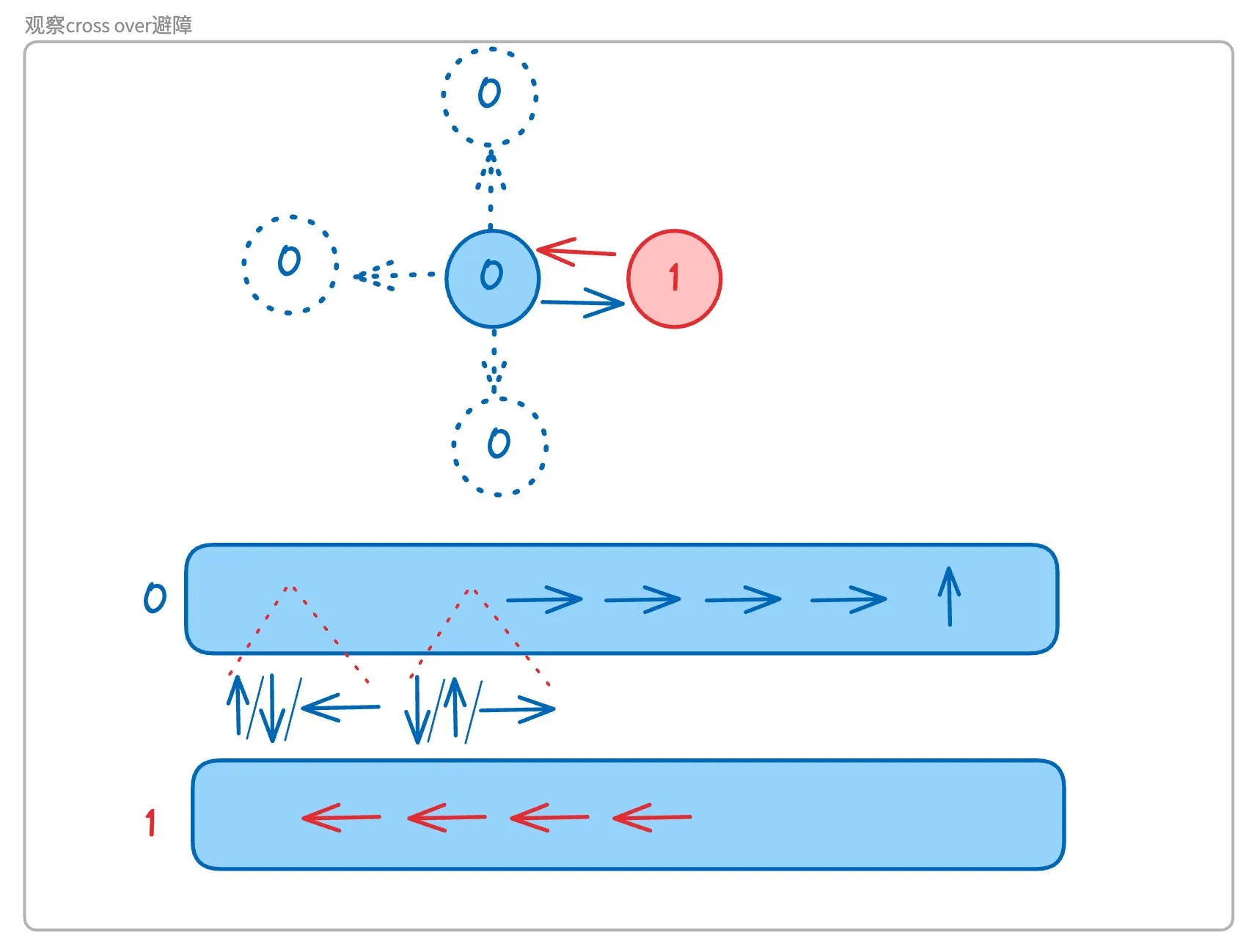
CleanShot 2024-03-26 at 19.57.17.jpg

如果0号机器人要向右走，却发现右侧的位置已经有一个1号机器人了，那么如果1号机器人下一帧的移动方向是向左，就判断会发生cross over。解决办法则是让0号机器人尝试向上、下、右侧避让，并在避让后插入一个相反的方向回到原来的位置。

这里要注意的点是，选择向哪个方向避让与为什么让0号机器人避让而不是1号机器人避让

首先看向哪个方向避让的问题，我们可以进行如下思考：

要选择可以走的方向避让，如果避让的那个方向是墙，则换一个方向
如果1号机器人在下一帧要向下移动，那么0号机器人本帧就不要向下避让了，因为如果0号机器人本帧向下避让，那么在下一帧依然会发生cross over，但如果0号机器人不向下避让，则之后就不会再次发生cross over。总而言之，避让的方向选择不与被避让机器人下一步方向相同的。
假如0号机器人排除掉了向下避让，还有向左向上两个方向进行选择，哪一个方向是更好的呢？我们发现0号机器人之后的路径中本就有一个向上的行走，如果我们发现向上避让，并不插入相反的方向让机器人回到避让前的位置，而是接着向右走四步，每一步都可以执行并且也能到达终点的话，那么选择向上避让就会节省两帧的时间。但如果不能满足这个条件的话，那么在当前已知信息下，向上避让与向左避让是同样优的。

再就是为什么让0号机器人避让而不是1号机器人避让的问题，这里涉及到了优先级的概念，暂时按下不表（这部分的设计insomnia并不是很清楚，等搞清楚了再补充）。

感谢评论区Zerol Acqua的补充

文章里提到的“碰撞的两种可能性”的逻辑，对于试探观察（实时）和整体调整（寻路时）的避障都是适用的。

然而，还有一种在目前代码（实现不健全的前提下）会出现的情况

一个机器人无法移动在发呆由于寻路、取货、卸货时，机器人有一帧或者多帧无法移动另一个机器人要往静止机器人所在的位置上移动由于存在固定的优先级，优先级高的往优先级停的静止机器人上移动寻路的结果，与避障的结果存到同一个路径队列 robotPaths[i] 中这样就存在一个问题，静止的机器人如果要躲避来袭的高优先级机器人，势必要往自己的路径队列里加入避障移动（一般是一来一回的移动）。假如这个静止的机器人正在寻路，此时发生避障行为就很麻烦，因为寻路随时会结束并往机器人路径里更新移动，那么就可能出现加入的避障移动被寻路结束得到的路径覆盖的问题。

同时，因为避障算法是在主线程 RobotWork() 中执行的，寻路则在分离的子线程中执行的。将两者的结果存在同一个路径队列中，会导致每次更新避障也要访问机器人的路径，那就必须扩大上锁的范围了

因此，在试探观察避障的实现中，将避障的移动路径与寻路的移动路径分别存在两个队列中。这种分离方式，既能避免路径覆盖的问题，又有助于缩小锁的作用范围。

通过整体调整规划进行避障

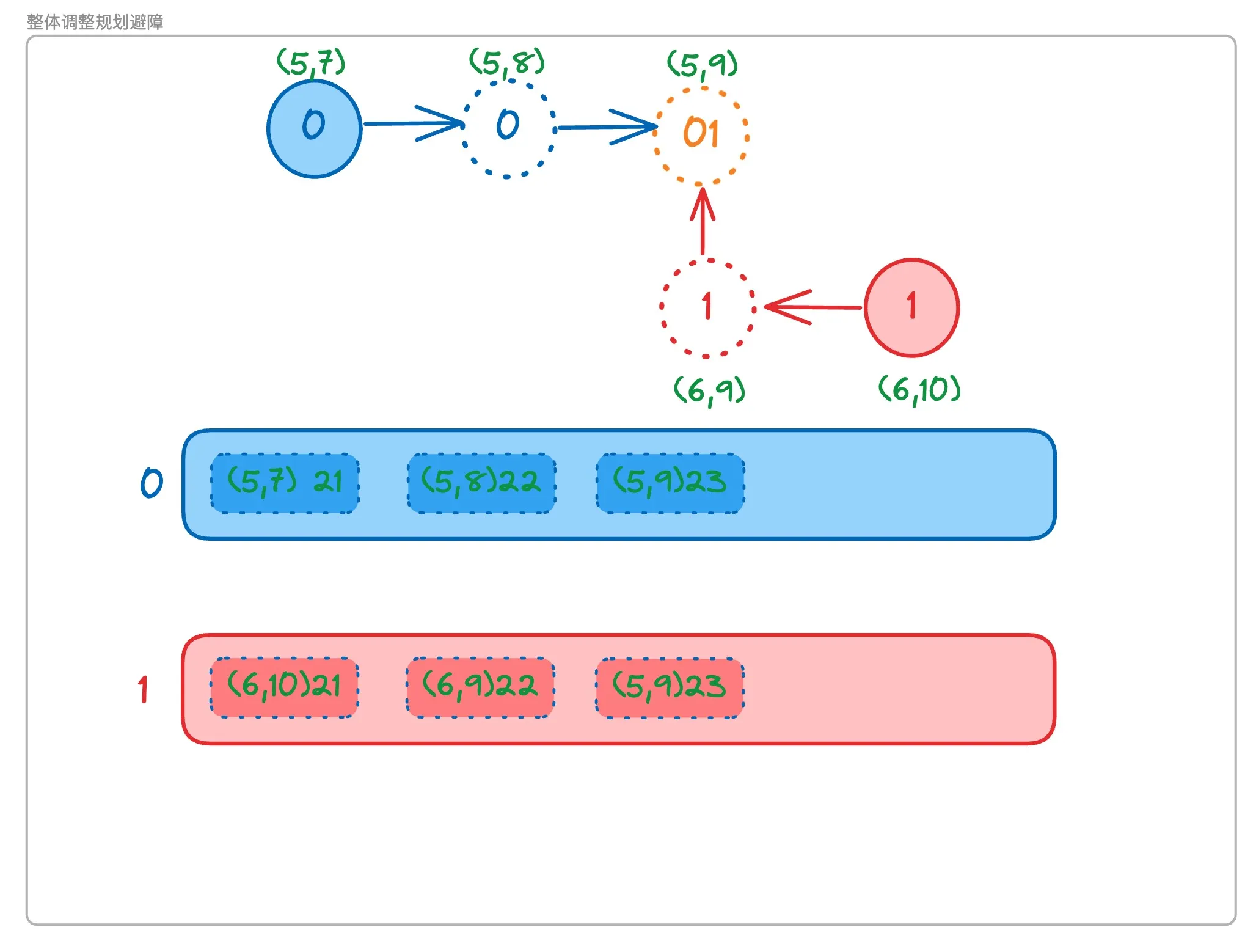
CleanShot 2024-03-27 at 17.22.05.jpg

如图所示，0号机器人与1号机器人的路径列表中都存放着xyt结构，即在t帧时刻，机器人将要前往的xy位置。根据xyt我们可以发现，如果0号机器人与1号机器人的路径列表中存在xyt都相同的节点，则说明会发生collision

找到了发生collision的位置，就可以通过插入静止帧等办法解决collision。

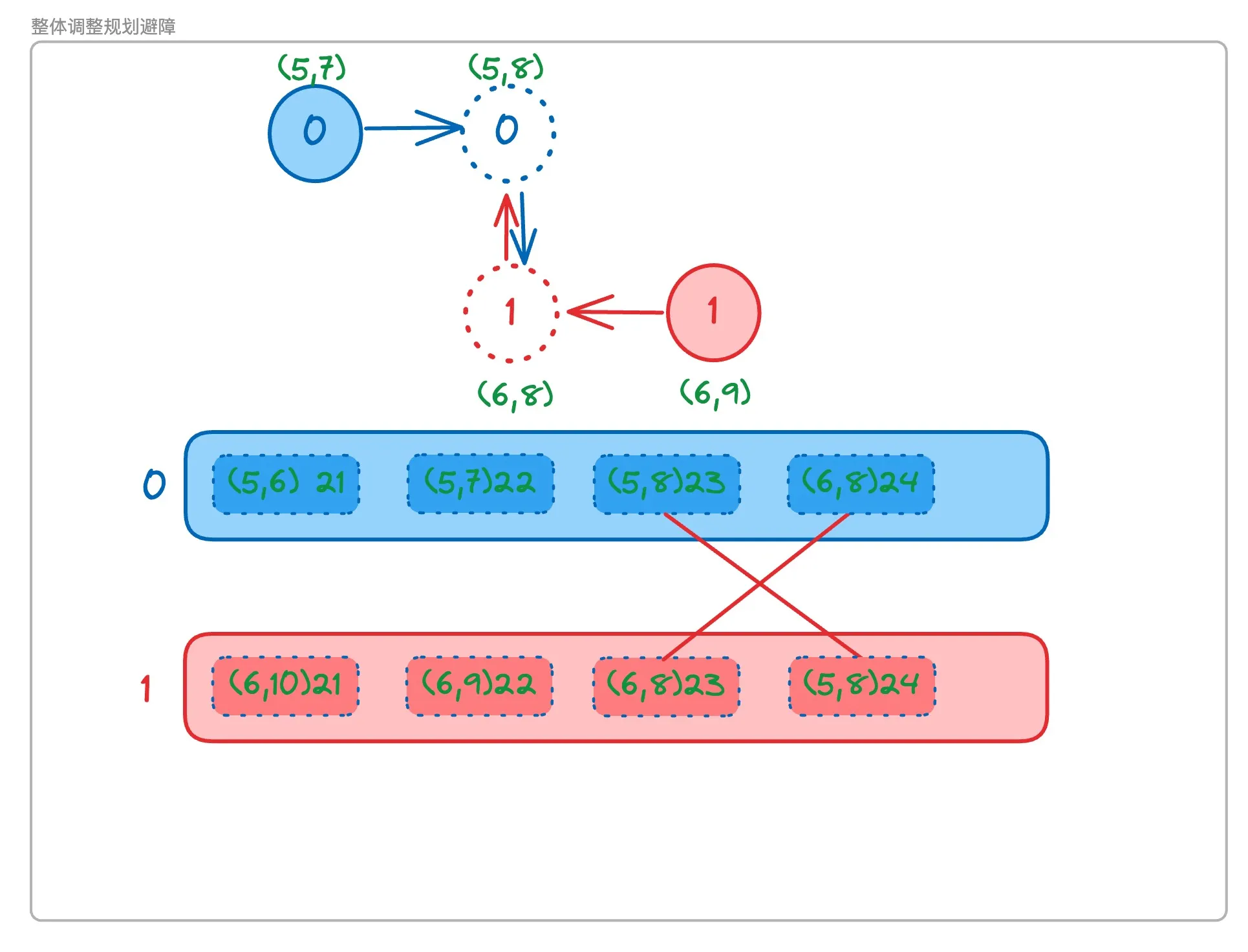
CleanShot 2024-03-27 at 17.32.35.jpg

如图所示，根据xyt我们可以发现，如果0号机器人与1号机器人的路径列表中存在t对齐而xy十字交叉相同的节点，则说明会发生cross over

我们可以在机器人的路径列表发生增长的时候对所有机器人的整个路径列表进行检查，查看是否存在collision与cross over的情况，并尝试解决。

这里要思考一个问题，尝试解决cross over与collision的过程中，我们是否会引入新的cross over或collision呢？

我个人认为，通过递归结构可以解决该问题。即，一次只尝试解决当前场面中存在的碰撞情况，尝试解决之后，立刻再次检测是否存在碰撞情况，并再次尝试解决，直到不再存在碰撞为止。

那么，感性上这么做是可行的，如何证明不断递归尝试解决碰撞，一定可以停机呢？（也即在经过有限次该过程后，场面总能达到不存在碰撞的情况）

关于如何保证不跳帧——Timer与WaitGroup结构

我们希望程序处理每一帧的用时尽量不超过15ms，即使超过了15ms也不能影响下一帧的信息读入与处理。

在go语言中有所谓的Timer结构，专门用于处理这种需求。

go
type Timer struct {
    C <-chan Time
    r runtimeTimer
}

func waitChannel(conn <-chan string) bool {
    timer := time.NewTimer(1 * time.Second) //设置超时时间 1s
    
    select {
    case <- conn:
        timer.stop() // 接收到数据后，要停止计时器
        return true
    case timer.C: //超时判断
        fmt.Println("WaitChannel timeout!")
        return false
    }
}

在这段代码中，Timer结构体是由一个channel与一个rutimeTimer构成的，rutimeTimer由go运行时接管，在到达指定的超时时间后向C这个channel中放入一个值。

在waitChannel函数中，select关键字会阻塞尝试从conn与timer.C中取出一个值，哪个channel中先有值，select就会执行对应的case代码，这样就保证了即使conn一秒后仍然没有值被放入，select也可以从timer.C中取出值，从而保证该函数的阻塞时长不会超过1s。

回到这次比赛的例子上，我们就是要在c++中实现类似的Timer结构的功能。

由于我们每个机器人都要开启一个单独的线程执行，所以一共会开很多个线程，这让人想到go中的WaitGroup结构。

go
func main() {
    var waitGroup sync.WaitGroup

    start := time.Now()
    waitGroup.Add(5)
    for i := 0; i < 5; i++ {
        go func() {
            defer waitGroup.Done()
            time.Sleep(time.Second)
            fmt.Println("done")
        }()
    }

    waitGroup.Wait()
    fmt.Println(time.Now().Sub(start).Seconds())
}

输出为

txt
done
done
done
done
done
1.000306089

在上面的代码中，waitGroup.Add(5)指定了要开启协程的数量，在协程内部，调用waitGroup.Done()将计数器减一，当waitGroup的计数器小于等于0时，解除waitGroup.Wait()的阻塞。

我们将waitGroup与Timer结构结合起来。也就是让解除waitGroup.Wait()阻塞的条件除了计数器小于等于0，还要加上超过了一段时间也解除阻塞。

用C++代码实现如下：

cpp
class WaitGroup {
private:
    std::mutex mtx;
    std::condition_variable cv;
    int count;
    size_t waitUntilOnMs;

public:
    WaitGroup(int initialCount, size_t waitUntil) : count(initialCount), waitUntilOnMs(waitUntil) {
    }

    void Add(int delta) {
        std::thread([this] {
            std::this_thread::sleep_for(std::chrono::milliseconds(waitUntilOnMs));
            unique_lock lock(mtx);
            count = 0;
        }).detach();
        unique_lock lock(mtx);
        count += delta;
    }

    void Done() {
        unique_lock lock(mtx);
        count -= 1;
        if (count <= 0) {
            count = 0;
            cv.notify_all();
        }
    }

    void Wait() {
        unique_lock lock(mtx);
        cv.wait(lock, [this] { return count <= 0; });
    }
};

可以看到，在上面的程序中，WaitGroup类中有一个计数器与一个计时器，当调用Add函数时，会开启一个线程作为计时器，当到达指定的时间时，将计数器重置为0，此时视为等同于调用了Done函数至计数器归零。

事件循环

整理一下整个过程中按照时间顺序的时间循环

世界初始化（读入地图与泊位初始信息）
利用初始化时间对地图做预处理
循环🔄
读入帧信息
根据帧信息更新场面数据
调整机器人的路径（耗时操作）
更新场面统计信息
判断拾取命令
判断卸货命令
移动命令
循环🔄

调整机器人路径算法

第一次取货

由于第一次取货是从机器人的初始位置出发，去寻找货物，再送到泊位，这部分的全局最优解应该满足，机器人到货物的距离+货物到最近泊位的距离最小（这里不考虑价值是因为第一次取货必定场上货物数量少于机器人数，所以不考虑价值），满足该条件则将机器人与该货物绑定，货物进入机器人的取货列表。

非第一次的取货

对于非第一次取货，总是从泊位出发，到距离目标货物最近的泊位结束，因此价值函数可以是

\forall(r,g)\quad\argmax_{(r,g)}\frac{g.value}{dist(r.xy, g.xy)+closest\_berth\_dist(g)}

其中 $r$ 为机器人， $g$ 为货物， $g.value$ 为货物 $g$ 的价值， $dist(r.xy, g.xy)$ 为机器人 $r$ 到货物 $g$ 的路径长度， $closest\_berth\_dist(g)$ 为货物到距其最近的泊位的距离

对选择货物-机器人对这一过程的抽象

我们发现，总是要对所有的 $(r,g)$ 进行遍历，对某一个价值函数进行计算，最后得到使得价值函数最大的 $(r,g)$ 对，因此对该过程抽象为一个函数。

目录